Calculateur de tolérance aux pannes Byzantines
Calculez le nombre minimum de nœuds nécessaires pour un système tolérant les pannes byzantines (BFT) selon la formule n ≥ 3f + 1.
La règle mathématique qui décide de la survie d’un réseau blockchain
Imaginons un réseau de nœuds qui doit prendre une décision ensemble : valider une transaction, mettre à jour un état, ou signer un bloc. Mais certains de ces nœuds mentent, se trompent, ou sont piratés. Comment le réseau continue-t-il à fonctionner ? La réponse se trouve dans une équation simple, mais puissante : n ≥ 3f + 1. C’est la règle de base de tout système tolérant les pannes byzantines (BFT). Elle ne dépend pas de la vitesse, ni de la puissance, ni du budget. Elle dépend uniquement du nombre de nœuds et du nombre de nœuds défaillants qu’on est prêt à accepter.
Que signifie n ≥ 3f + 1 ?
Chaque lettre de cette formule a un sens précis. n est le nombre total de nœuds dans le réseau. f est le nombre maximum de nœuds qui peuvent être défaillants - c’est-à-dire qu’ils envoient des messages contradictoires, se comportent mal, ou sont hors ligne. La formule dit : pour que le système reste fiable, vous devez avoir au moins trois fois plus de nœuds défaillants que le nombre de pannes que vous voulez tolérer, plus un nœud de plus pour faire la différence.
Exemple simple : si vous voulez tolérer 1 nœud défaillant (f=1), vous avez besoin de 4 nœuds au minimum (n=4). Pour tolérer 2 nœuds défaillants (f=2), vous avez besoin de 7 nœuds. Pour 3 pannes, vous en avez besoin de 10. Et ainsi de suite. Ce n’est pas une suggestion. C’est une preuve mathématique. Si vous avez moins que ça, il est impossible de garantir que les nœuds honnêtes atteindront un consensus.
Pourquoi 3f + 1 ? Pas 2f + 1 ?
Beaucoup pensent que si un nœud ment, il suffit d’avoir deux nœuds honnêtes pour le contredire. Mais le problème byzantin est plus sournois. Un nœud malveillant ne dit pas la même chose à tout le monde. Il envoie un message à la moitié du réseau, un message opposé à l’autre moitié. Si vous n’avez que 3 nœuds et qu’un seul est défaillant, il peut convaincre deux nœuds honnêtes de choisir deux décisions différentes. Résultat : blocage total.
La formule 3f + 1 garantit que même si les nœuds malveillants envoient des messages contradictoires, les nœuds honnêtes seront toujours en majorité absolue. Avec 4 nœuds et 1 défaillant, vous avez 3 nœuds honnêtes. Même si le nœud défaillant envoie deux messages différents, les trois honnêtes peuvent comparer leurs messages, détecter l’incohérence, et rejeter la mauvaise information. C’est ce qu’on appelle le majority voting avec vérification croisée. Et cette logique se maintient à n’importe quelle échelle.
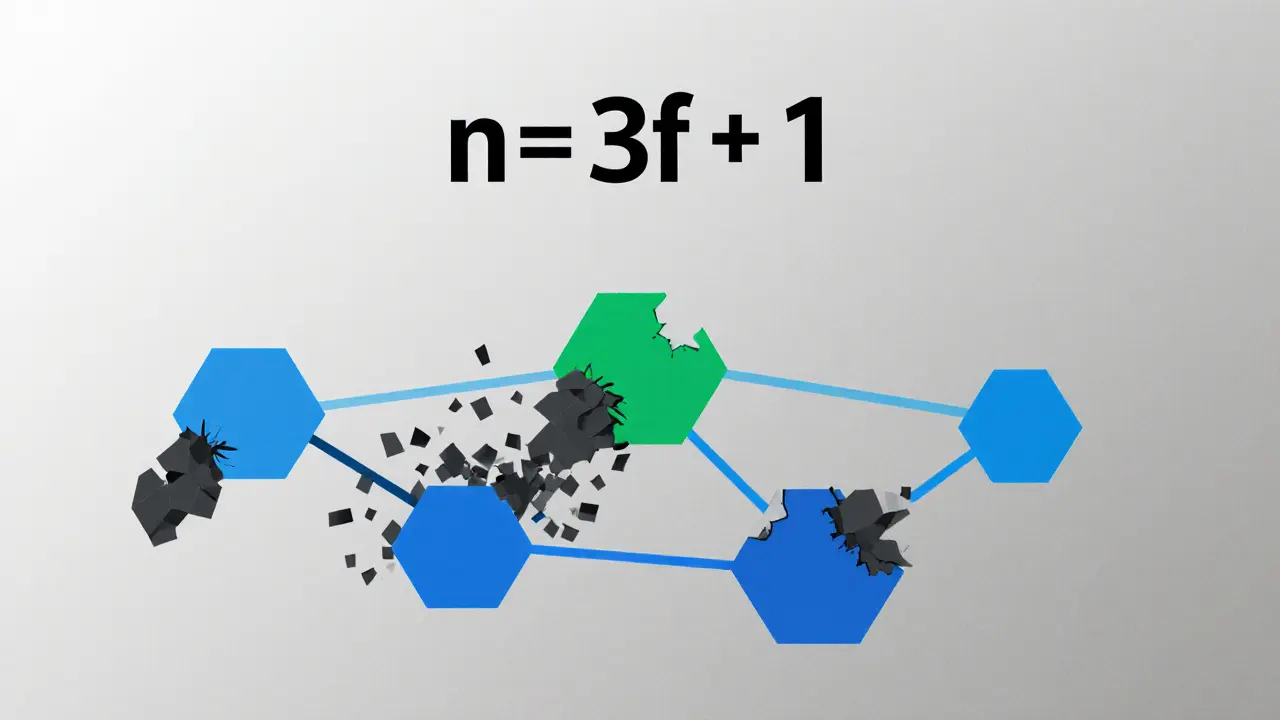
Combien de pannes réelles un réseau peut-il supporter ?
Voici un tableau clair avec les configurations les plus courantes :
| Nombre de nœuds défaillants tolérés (f) | Nombre minimum de nœuds (n) | Pourcentage de nœuds défaillants |
|---|---|---|
| 1 | 4 | 25% |
| 2 | 7 | 28,6% |
| 3 | 10 | 30% |
| 4 | 13 | 30,8% |
| 5 | 16 | 31,25% |
Remarquez quelque chose ? Le pourcentage de nœuds défaillants tolérés ne dépasse jamais 33,3%. C’est la limite théorique. Même avec 1000 nœuds, vous ne pouvez pas tolérer plus d’un tiers de pannes. C’est une loi de la physique des systèmes distribués, comme la vitesse de la lumière pour la physique classique.
Les systèmes réels qui utilisent cette règle
La plupart des blockchains permissionnées - c’est-à-dire celles où les participants sont connus et approuvés - utilisent BFT. Hyperledger Fabric, par exemple, exige au moins 4 nœuds pour son mécanisme de consensus. Pourquoi pas 3 ? Parce que 3 nœuds ne peuvent pas tolérer une seule panne. Avec 3 nœuds et 1 défaillant, il reste 2 nœuds. Et 2 nœuds ne peuvent pas décider ensemble s’ils ne se font pas confiance. Le système s’arrête.
Les systèmes aérospatiaux de la NASA utilisent des configurations à 7 nœuds pour tolérer 2 pannes simultanées. JP Morgan utilise 10 nœuds dans Quorum pour tolérer 3 pannes dans ses réseaux financiers. L’Union européenne, avec sa loi DORA de 2024, exige que les infrastructures financières puissent tolérer au moins 2 pannes byzantines - ce qui signifie que vous devez avoir au moins 7 nœuds.
En revanche, Bitcoin et Ethereum n’utilisent pas BFT. Bitcoin utilise le Proof-of-Work : il tolère jusqu’à 49% de puissance de hachage malveillante, mais cela prend des minutes, voire des heures, pour confirmer une transaction. Ethereum 2.0 utilise un mécanisme de consensus proche du BFT (Casper FFG), mais il exige des centaines, voire des milliers de nœuds, pour compenser la nature ouverte du réseau. BFT, lui, est fait pour les réseaux contrôlés, pas pour les réseaux ouverts.
Les pièges pratiques : pourquoi 4 nœuds ne suffisent pas en production
Techniquement, 4 nœuds suffisent pour tolérer 1 panne. Mais en pratique, c’est extrêmement risqué. Pourquoi ? Parce qu’un nœud peut tomber en panne pendant une mise à jour, une coupure d’électricité, ou une attaque réseau. Si vous avez exactement 4 nœuds et qu’un seul tombe, il vous reste 3 nœuds. Et 3 nœuds, c’est le seuil critique : vous êtes à la limite de la tolérance. Si un deuxième nœud tombe - même pour 5 minutes - le réseau s’arrête. Plus de consensus. Plus de transactions. Plus rien.
Les entreprises qui ont essayé de démarrer avec 4 nœuds racontent des histoires de downtime de 72 heures. Ce n’est pas une erreur technique. C’est une erreur de conception. La règle de 3f + 1 est la limite minimale. En production, vous devez toujours ajouter un nœud de sécurité. Donc, pour tolérer 1 panne, utilisez 5 nœuds. Pour tolérer 2 pannes, utilisez 8 ou 9 nœuds. Ce n’est pas une exigence théorique. C’est une règle de bon sens.
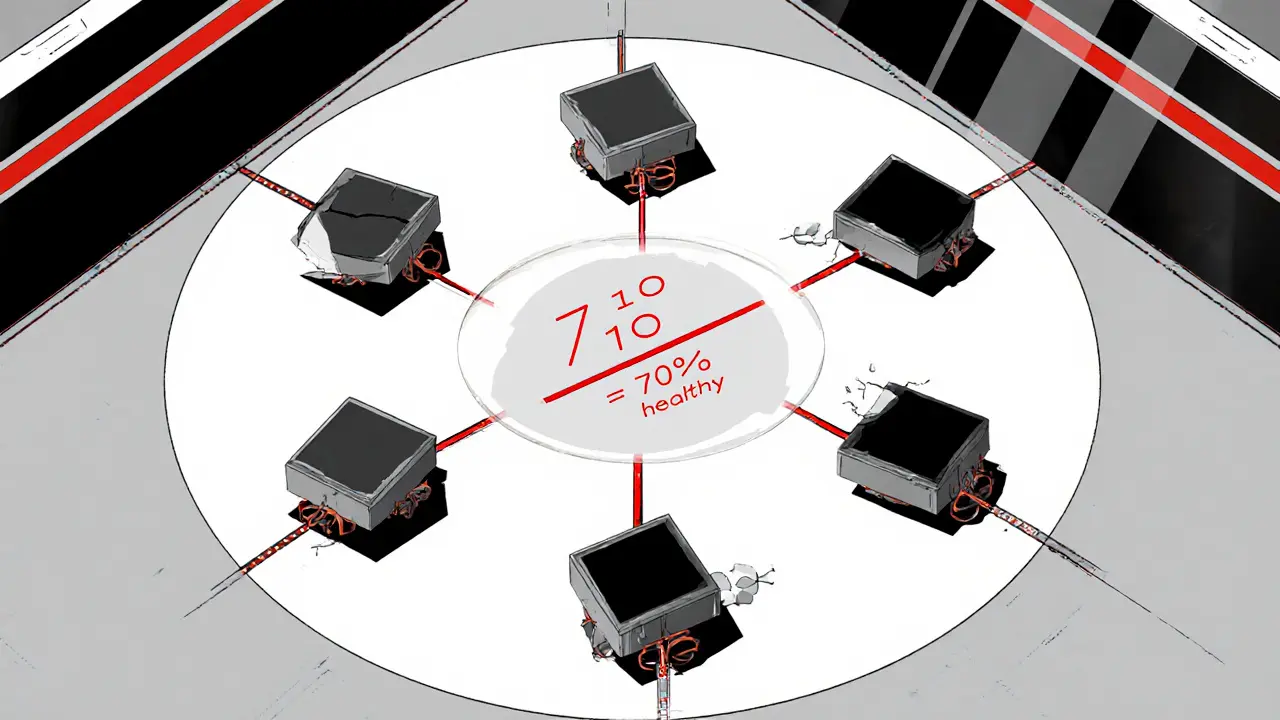
Les limites et les futurs possibles
Le BFT est puissant, mais il a des défauts. Il est coûteux : chaque nœud doit exécuter des signatures cryptographiques, échanger des messages en trois tours, et vérifier chaque réponse. Cela ralentit le réseau. Une étude du MIT a montré que lorsque 3 nœuds sur 10 deviennent défaillants, la latence augmente de 227%.
Il est aussi rigide. Vous ne pouvez pas ajouter ou retirer des nœuds facilement. Si vous avez 7 nœuds et que vous voulez en ajouter un 8e, vous devez redémarrer tout le système. Certains projets comme Apache BFT-SMART 2.0 tentent de résoudre ce problème avec une reconfiguration dynamique, mais c’est encore complexe.
La recherche avance. Des équipes comme celles du MIT ont exploré des versions « fractionnaires » du BFT, où la tolérance devient probabiliste, pas déterministe. Mais pour les systèmes critiques - banques, aérospatiale, santé - on ne veut pas de probabilités. On veut une garantie absolue. Et pour ça, il n’y a toujours qu’une seule réponse : n ≥ 3f + 1.
Comment choisir le bon nombre de nœuds pour votre projet
- Déterminez combien de pannes vous pouvez tolérer. Pour une application interne, 1 panne (f=1) suffit. Pour une infrastructure financière, visez 2 pannes (f=2).
- Calculez le nombre minimum de nœuds : n = 3f + 1.
- Ajoutez un nœud de sécurité : passez à n = 3f + 2 ou 3f + 3.
- Assurez-vous que chaque nœud est géographiquement et techniquement indépendant. Un seul fournisseur cloud pour tous les nœuds ? C’est une faiblesse.
- Testez les pannes réelles. Faites tomber un nœud pendant une transaction. Vérifiez que le système continue.
Si vous commencez avec trop peu de nœuds, vous ne serez jamais sûr. Si vous en avez trop, vous ralentissez votre réseau. Le bon équilibre se trouve entre la théorie et la réalité pratique.
Les erreurs courantes à éviter
- Croire que 3 nœuds peuvent tolérer 1 panne. C’est impossible.
- Utiliser des nœuds sur le même serveur ou le même fournisseur. Cela crée un point de défaillance unique.
- Ignorer les certificats cryptographiques. 89% des pannes BFT viennent d’une mauvaise configuration des clés.
- Penser que BFT est bon pour les blockchains publiques. Il ne l’est pas. Il est fait pour les réseaux fermés.
- Ne pas prévoir de plan de reprise après panne. Si vous perdez plus de f nœuds, le système est mort. Vous devez avoir un processus pour en ajouter de nouveaux.
Peut-on tolérer plus d’un tiers de nœuds défaillants avec une meilleure technologie ?
Non. La limite de 33,3% de nœuds défaillants est une preuve mathématique, pas une limitation technique. Même avec des algorithmes ultra-rapides ou des cryptographies quantiques, vous ne pouvez pas contourner ce seuil. C’est une loi fondamentale des systèmes distribués. Toute affirmation contraire est soit une erreur, soit une simplification trompeuse.
Pourquoi Bitcoin ne utilise-t-il pas BFT ?
Bitcoin utilise le Proof-of-Work, qui permet à n’importe qui de rejoindre le réseau. BFT, en revanche, exige que tous les nœuds soient connus et authentifiés à l’avance. Dans un réseau ouvert comme Bitcoin, il est impossible de savoir qui est un nœud honnête et qui est malveillant. Le PoW résout ce problème en rendant l’attaque coûteuse en énergie, pas en limitant le nombre de participants.
Un réseau avec 5 nœuds peut-il tolérer 2 pannes ?
Non. Avec 5 nœuds, vous pouvez tolérer au maximum 1 panne (car 3×1 + 1 = 4, et 5 > 4). Pour tolérer 2 pannes, vous avez besoin d’au moins 7 nœuds. Si vous avez 5 nœuds et que 2 tombent, il reste 3 nœuds. Et 3 nœuds ne peuvent pas distinguer si les deux nœuds manquants sont défaillants ou simplement hors ligne. Le système s’arrête.
Quelle est la différence entre PBFT et BFT ?
BFT est le concept général de tolérance aux pannes byzantines. PBFT (Practical Byzantine Fault Tolerance) est une implémentation concrète, créée en 1999, qui rend cette tolérance efficace pour les systèmes réels. Tous les systèmes BFT modernes - comme ceux de Hyperledger, Hedera ou Quorum - sont des variantes de PBFT. Donc, PBFT est un type de BFT, pas une alternative.
Est-ce que les blockchains publiques comme Ethereum 2.0 utilisent BFT ?
Ethereum 2.0 utilise un protocole appelé Casper FFG, qui est basé sur des principes BFT, mais il ne respecte pas la règle n ≥ 3f + 1 de manière classique. Il utilise des milliers de nœuds pour compenser la nature ouverte du réseau. À chaque instant, il ne considère qu’un sous-ensemble de nœuds pour le consensus. C’est une forme de BFT adaptée, mais pas la même que celle des réseaux permissionnés.
Baptiste rongier
novembre 2, 2025 AT 08:41Merci pour le rappel.
yves briend
novembre 3, 2025 AT 22:27Louis Karl
novembre 5, 2025 AT 14:59Beau Payne
novembre 6, 2025 AT 17:25La preuve mathématique, c’est pas une option. C’est la base.
Et oui, 4 nœuds c’est du bricolage. En production, j’utilise toujours 5 pour 1 panne. C’est pas cher, c’est juste intelligent. 💪
Sabine Petzsch
novembre 6, 2025 AT 19:25J’ai vu une startup faire ça… et hop, 72h d’arrêt. C’est pas une erreur technique, c’est un crime contre la logique. 😅
Laurent Beaudroit
novembre 8, 2025 AT 01:15Marc Noatel
novembre 9, 2025 AT 13:43Aude Martinez
novembre 11, 2025 AT 04:35René Fuentes
novembre 13, 2025 AT 00:54J’ai fait tomber deux… et ça a planté.
C’est exactement ce qui est dit ici.
Pas de mystère. Juste de la logique.
Et oui, ajouter un nœud de sécurité, c’est pas une option. C’est une nécessité.
J’ai perdu 3 jours à cause de ça une fois… j’ai jamais répété l’erreur.
Martine Caillaud
novembre 14, 2025 AT 04:37Et puis, qui va gérer ça ? Un admin qui lit ce post ?
La réalité, c’est que 90% des projets BFT sont mal configurés… et personne ne veut l’admettre.
On préfère dire ‘c’est la faute de la blockchain’ plutôt que ‘on a été paresseux’.